5 loginiai galvosūkiai šablonams rasti

Vietoj klaustuko apskritime turėtų būti skaičius 253. Tai principas, pagal kurį formuojami skaičiai apskritimuose: kiekvienas ankstesnis padauginamas iš 2 ir prie rezultato pridedama 3.

1 × 2 + 3 = 5.
5 × 2 + 3 = 13.
13 × 2 + 3 = 29.
29 × 2 + 3 = 61.
61 × 2 + 3 = 125.
125 × 2 + 3 = 253.

Arba čia yra kitas sprendimo būdas: prie kiekvieno ankstesnio skaičiaus prie n-osios galios pridedama 2.

1 + 2² = 1 + 4 = 5.
5 + 2³ = 5 + 8 = 13.
13 + 2⁴ = 13 + 16 = 29.
29 + 2⁵ = 29 + 32 = 61.
61 + 2⁶ = 61 + 64 = 125.
125 + 2⁷ = 125 + 128 = 253.

Vietoje klaustuko kvadrate turėtų būti raidė „P“. Kiekvieno kvadrato skaičių suma yra raidės abėcėlėje eilės numeris. Patikrinkime:

6 + 4 + 4 = 14. „M“ yra keturioliktoji abėcėlės raidė. Mes taip pat skaičiuojame „Yo“!
4 + 1 + 7 = 12. „K“ yra dvylikta abėcėlės raidė.
5 + 6 + 10 = 21. „U“ yra dvidešimt pirmoji raidė abėcėlėje.
1 + 14 + 2 = 17. „P“ yra septynioliktoji abėcėlės raidė, kuri turėtų būti klaustuko vietoje.

Vietoj klaustuko turėtų būti skaičius 179. Jei judate pagal laikrodžio rodyklę nuo 3, tada kiekvienas paskesnis skaičius yra lygus dvigubai ankstesniam, prie kurio buvo pridėti 1, 3, 5, 7, 9.

3 × 2 + 1 = 7.
7 × 2 + 3 = 17.
17 × 2 + 5 = 39.
39 × 2 + 7 = 85.
85 × 2 + 9 = 179.

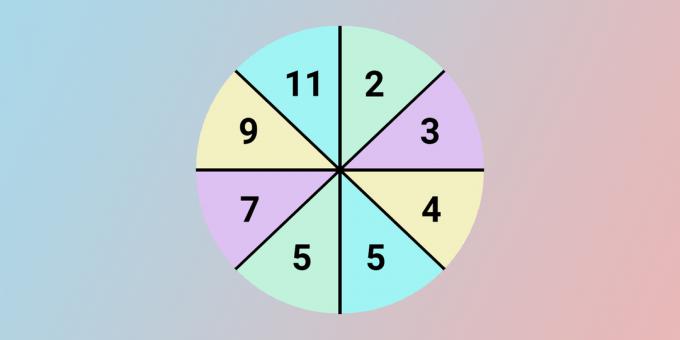
Vietoj klaustuko turėtų būti skaičius 11. Norėdami gauti kiekvieną skaičių iš kairės apskritimo pusės, paimame skaičių iš priešingo sektoriaus, padvigubiname ir pridedame vieną.

5 = 2 × 2 + 1.
7 = 3 × 2 + 1.
9 = 4 × 2 + 1.
11 = 5 × 2 + 1.

Vietoj klaustuko skaičius turėtų būti 66. Jei judėsite pagal laikrodžio rodyklę nuo 4, kiekvienas paskesnis skaičius bus lygus dvigubai ankstesniam, iš kurio buvo atimti du.

4 × 2 − 2 = 8 − 2 = 6.
6 × 2 − 2 = 12 − 2 = 10.
10 × 2 − 2 = 20 − 2 = 18.
18 × 2 − 2 = 36 − 2 = 34.
34 × 2 − 2 = 68 − 2 = 66.