Įdomios matematikos faktai tiems pasaulio nori daugiau sužinoti apie

Layfhaker susimąstėte, kaip svarbu matematika yra mūsų kasdieniame gyvenime. Ar tai ne visi tą dar reikia? Atsakymas į šį klausimą būtų atsakyta rado į Nelly litvakų ir Andrew Raigorodskii "Kam to reikia matematikos knygos? Suprantama knyga apie tai, kaip skaitmeninis pasaulis. "

Ką ši knyga?

Apie matematikos. :) Tiksliau, iš šių jai skyriuose, kurie yra didžiausią paklausą logistikos, transporto tvarkaraščius, šifravimo ir kodavimo duomenų. Autoriai turimais pavyzdžiais parodyti, kaip matematika padeda taupyti laiką ir pinigus, išsaugokite duomenis pagal patikimą apsaugą ir pasirinkite parduotuvėje eilėje.

Kas yra tiesinis programavimas

Šiuo atveju mes kalbame ne apie programavimo savaime. Tai gana optimizavimo procesas. Kodėl linijinis? Kadangi mes kalbame tik apie tiesinių lygčių: kai kintamieji pridėti, atimti ar dauginti numeris. Nėra exponentiations ar daugybos operacijas. Toks programavimas padeda sumažinti prekių ar paslaugų kaina (jei kalbame apie prekybą) arba padidinti pajamas.

Tiesinis programavimas naudojami naftos pramonėje, taip pat logistikos, planavimas, planavimas.

Trumpai tariant, kaip, pavyzdžiui, jis atrodo.

Įsivaizduokite, kad esate užsiima metalo lakštų pardavimo. Vienas klientas įsakė jums 70 lapų, o antrasis - 30 lapų. Tokiu atveju, jūsų rezervai yra laikomi įvairiuose sandėliuose, iš kurių kiekviena turi mažiau nei 100 lapų. Jūsų užduotis - sumažinti pervežimo skardos klientams išlaidas.

Čia ateina į žaidimą linijinis lygtis. Mes nekalbame išsamiai, kaip ši problema buvo išspręsta knygoje, bet po kelių žingsnių skaičiavimai yra geriausias variantas, kuri leidžia jums išsaugoti 12% pristatymo kaina, palyginti su sąnaudomis, būtų patirti, jei nenorite naudoti matematinis požiūris.

Dabar įsivaizduokite, kad tai ne apie kelių lapų skardos pristatymo ir pagal tvarkaraštį ir sunkiųjų geležinkelių eismo visoje šalyje. Ir tada 12% - tai yra kelių nulių gale numeris.

Kodėl geriausia išeitis ne visada yra patogiausia?

Matematika - tikslios ir gražus mokslas. Tačiau ne visada yra problemų sprendimas atrodo gana tinkamas. Tai atsitiko su geležinkelio transporto Nyderlandų grafiką. Šioje nedidelėje šalyje mokyti ir traukiniai yra labai populiarus. Transporto tvarkaraštis yra toks pasenęs, kad yra bręsti buvo tikras sutraukti.

Todėl buvo nuspręsta parengti naują tvarkaraštį 2002 m. Ekspertai turėjo puikiai galvoti apie automobilių skaičių, sustojimų, lėktuvų pakilimo ir nusileidimo laikus, jau nekalbant traukinių vairuotojų ir konduktorių grafiką 5500 traukiniais per dieną.

Kaip rezultatas, idealus iš matematiniu požiūriu, grafikas buvo sudarytas. Ir kaip ir visi turi būti laimingi. Bet ne keleiviai: stotelė per trumpas, per vagonai pakraunami, jokio komforto. Tai atsitiko todėl, kad matematikos išspręsti tik matematines problemas. Ir kas kaltas, kad vadyba yra nevykęs?

Ar galima koduoti nieko?

Paprastosios kompiuterių vartotojams sunku įsivaizduoti, kad visi vaizdai, video, tekstai, dainos - tai ne vaizdai, video, tekstai ir dainos kaip ir nulių, ir nulių.

Koduoti tekstą lengviau, nes kiekviena raidė, skaitmuo arba skyrybos ženklas sugalvoti su ir nulių seką. Bet kas apie spalvą? Laimei, fizikai atrado, kad kiekviena spalva - tai raudonos, mėlynos ir žalios spalvos derinys. Ir tai reiškia, kad ir spalvos gali būti konvertuojamos į numerius.

Kiekviena spalva turi 255 atspalvių. Pavyzdžiui, oranžinė - raudona 255 ir 128 žalios, mėlynos - 191 žalios ir 255 mėlynos spalvos. O jei spalva gali būti išreikšti skaičiais, tai reiškia, kad jis gali būti dedamas į bet kurio kompiuterio, televizoriaus ar mobiliojo telefono.

Su video dar sunkiau - per daug informacijos. Tačiau matematikai rado išeitį iš šios situacijos ir išmoko suspausti duomenis. Pirmas kadras filmas yra užkoduota visiškai, tada koduojama tik keičia.

Problemos buvo tik su muzika. Mokslininkai vis dar neišmoko, kaip koduoti muzikos taip, kad jis skambėjo taip aišku, kaip ir gyvenime. Kadangi muzika negali būti išplėsta į "atspalvių", kurios gali būti parašytas skaitmeninėje srityje.

Kodėl internetas niekada pertraukos?

Ne, tai nėra Jūsų teikėjų, kurie kartais gali būti geriau dirbti. Tai apie tai, kodėl, pavyzdžiui, "Google" visada reaguoja į mūsų paklausimus, kodėl mes galime visada prieiga į dešinę vietų, ir kodėl trukdžiai (ir yra tikrai daug) nenutraukite mūsų prieigą prie World Wide Web.

Trumpas atsakymas į šį klausimą yra praėjusio amžiaus viduryje, du matematikas Paulius Erdos ir Alfredas Renas atvėrė pasaulio atsitiktinius grafikus. Skaičius - Šis paveikslėlis mazgų sujungtų linijų. Dabar įsivaizduokite, kad vienetų - kompiuterio, o linijos - ryšio linijos. Pavartojus suskaičiuokite iki 100 kompiuterių, jis atrodys taip:

Ir Renas ir Erdash ginčyti humanitarams ir skaičiavimo paprasta technikai atėjo į apsvaiginimo sudarymo. Kuo daugiau tinklo kompiuteriuose, tuo daugiau tarp jų nuorodos, tuo mažiau tikėtina, kad sukelti žalingų trikdžių, tai yra vienas, kad bus pleiskanoti mus iš neribotos bendravimo ir begalinis informacijos pasaulyje.

Jei netiki manimi, čia yra lentelė.

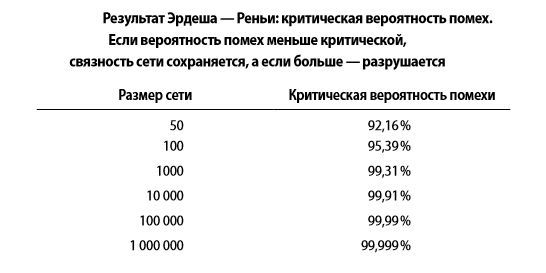
Tai yra, jei kai kanalas neveikia, beveik visada galima eiti į kitą kanalą ir susisiekti su nagrinėjamo veidrodį.

Kas yra internete, ir kaip to išvengti vieta?

Ar žinote, kad kiekvieną kartą, prašydami Google ar ketinate bet kokios svetainės, jums rasti sau tokioje vietoje? Žinoma, jis juda kur kas greičiau, nei tuo metu prekybos centruose kasos, ir jūs beveik nepastebi nutraukimo, tačiau, jei kas nors padarė per pasaulio užklausa reikalauja daugiau laiko ant jo apdorojimas.

Taigi jums reikia pasirinkti serverį, kurioje visi mažiausias, arba vienas eilėje prie kurio nėra sunkiųjų užklausą.

Ir čia įsigalios paprastai yra dvi pasirinkimo. Informatikos Derekas trokšta Edwardas ir Johnas Lazovsky Zahordzhan 1986 ir pasiūlė įrodyti teoriją, kad jei apriboti serverių asortimentą, kuris bus išsiųstas į jūsų prašymą, iki dviejų, tada slydimo ruožtu padidina tikimybę kartais.

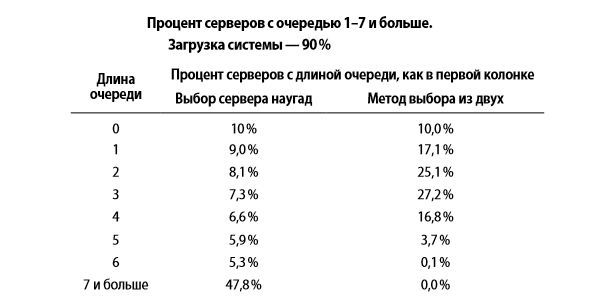
Pažvelkime į prekybos centrą pavyzdyje. Prieš jums fondų su skirtingais linijos ilgis daug. Jūs turite variantų: atsitiktinai pasirinkti pirmasis prieinamas arba sustabdyti dviejų ir pasirinkti vieną, kurioje visi mažiau. Taigi jūs greičiau užbaigti pirkimo su didesne tikimybe.

Iš keturių Rankos paspaudimai teorija

Daugelis yra girdėję, kad visi pasaulio žmonės yra susipažinę su vienas kitą po šešių Rankos paspaudimai. Ši teorija dar 1960 parodė, sociologas Stanley Milgram, klausia žmonės iš skirtingų narių nusiųsti laišką vienam asmeniui. Laiškas buvo pirmasis nusiųsti savo draugui, kuris savo ruožtu išsiuntė ją - ir taip tol, kol laiško niekada pasiekė adresatą. Kaip rezultatas, grandinė buvo tik šeši.

Tai buvo ne iki tol, kol "Facebook" darbuotojai nėra skirtas mokslininkų kartą patvirtinti arba paneigti šią teoriją. Po perdirbant visas įmanomas poras pažįstamų tarp visų tinklo vartotojų, paaiškėjo, kad ši grandinė yra dar trumpesnis. Ir tai yra tik 4.7! Ar galite įsivaizduoti? Tarp bet žmogus žemėje, ir jūs tik 4,7 Handshake!

Turėčiau skaityti šią knygą?

Taip, jei taip pat norite žinoti, kaip duomenų šifravimas, kuris įveikė kodą "Enigma", nes yra Reklamos aukcionus "Google" ir "Yandex" ", taip pat giliau į matematinės problemos ir lygtis pasaulis.

Layfhaker sakiau jums ne visus įdomių faktų pramogas matematikos, todėl, jei jus norite papildyti savo žinias šioje srityje, knyga "Kas turi matematikos" tikrai įrodyti jums naudinga.

Nepaisant pateikimo paprastumo, jei esate humanitarinė, o skaitymas, jums gali tekti matematinį vadovėlį.

Pirkti spausdintą knygaPirkti e-knyga